Determinazione della numerosità campionaria

Introduzione

Una delle domande che tipicamente si sentono rivolgere statistici ed epidemiologi quando un clinico si accinge a scrivere il protocollo di uno studio è relativa al numero di soggetti da arruolare nel campione che dovrà studiare. Prudentemente, ma del tutto correttamente, la risposta che essi gli daranno non potrà che essere: dipende. Infatti il calcolo della numerosità campionaria è abbastanza complicato e necessita della disponibilità di diverse informazioni. In fase di pianificazione di uno studio è di fondamentale importanza mettere in relazione la dimensione campionaria con un grado di precisione prefissato (1).

Scopo del presente articolo è fare una sintesi dei criteri alla base del calcolo della numerosità campionaria e mostrare alcuni esempi di metodi per determinare la dimensione di un campione.

Criteri

In linea di massima si può affermare che il principio su cui si fonda il calcolo della dimensione campionaria è quello di rendere massima la probabilità di individuare la presenza di un effetto (protettivo o nocivo) di un trattamento e/o di un intervento con ragionevole certezza, cioè in maniera statisticamente significativa.

In generale, più grande è il campione, più precisi e attendibili saranno i risultati, a patto che il campionamento sia realizzato con un metodo corretto e sapendo che indagini su campioni di grandi dimensioni sono più costose e richiedono più tempo. Come sempre in medio stat virtus. I soggetti arruolati devono essere di numerosità sufficiente affinché un effetto clinicamente significativo lo sia anche dal punto di vista statistico. Anche se meno frequentemente, si può verificare il problema opposto, vale a dire che si arruoli un numero di soggetti talmente elevato da rendere statisticamente significativo un effetto privo di significatività clinica.

A questo riguardo l’arruolamento di un numero adeguato di soggetti ha anche una rilevanza etica che deve essere tenuta in considerazione quando si progetta una ricerca. Infatti, uno studio sottodimensionato che, pertanto, molto probabilmente non consentirà un progresso nelle conoscenze scientifiche, potrebbe esporre inutilmente delle persone a interventi potenzialmente rischiosi; analogamente, uno studio sovradimensionato esporrebbe ai medesimi rischi un numero ancor più grande di persone al solo fine di conferire a un effetto osservato una significatività statistica che surroghi quasi artificiosamente la difficile dimostrazione di una chiara significatività clinica.

Senza contare che sottodimensionare o sovradimensionare uno studio ha anche implicazioni economiche; nel primo caso si sprecano risorse per effettuare uno studio che già in partenza ha poche possibilità di dimostrare la presenza di un effetto; nel caso invece di uno studio sovradimensionato, il consumo non necessario di risorse si verifica sostanzialmente per definizione.

Nel precedente articolo (2), nel quale era stata fatta una breve rassegna di alcuni esempi di campionamento probabilistico e non probabilistico, si introduceva il problema della scelta della dimensione campionaria, cruciale per il successo di uno studio analitico.

Alla base del calcolo della dimensione campionaria appropriata vi è proprio la necessità di riuscire a cogliere in maniera statisticamente significativa la più piccola differenza rilevante dal punto di vista clinico tra i trattamenti in studio. Per questo motivo, al fine del corretto dimensionamento di un campione è indispensabile che il clinico definisca in maniera esplicita, anche in termini quantitativi, quali sono gli obiettivi che lo studio si prefigge; in particolare, quant’è la differenza che si aspetta di osservare tra i gruppi a confronto, ad esempio quanto miglioramento ci si aspetta da una nuova terapia da introdurre rispetto a chi assume farmaci già correntemente utilizzati. Va da sé che l’entità dell’effetto di interesse da rilevare negli studi comparativi è molto importante, in quanto se si desidera rilevare una piccola dimensione dell’effetto è necessario un campione più grande. Ad esempio, se aumenta la distanza assoluta tra la media dell’ipotesi nulla e la media proposta per l’ipotesi alternativa, il campione necessario si riduce. A tal fine è indispensabile avere una stima del parametro nel gruppo di controllo rispetto a quello al quale viene ad esempio somministrata la nuova terapia oggetto dello studio.

Anche la varianza dell’esito nella popolazione in studio è fondamentale nella determinazione della dimensione campionaria, in quanto più la varianza è grande, maggiore sarà la numerosità richiesta. Nel precedente articolo, oltre ad accennare anche a questo aspetto, si faceva riferimento ad altri parametri, a partire dalle due tipologie di errore che si possono commettere nel testare le ipotesi di uno studio. In particolare: l’errore di tipo I (α), commesso quando si rifiuta l’ipotesi nulla H₀ della non differenza tra gruppi a confronto, per affermare la presenza di una differenza in realtà inesistente; l’errore di tipo II (β), commesso quando si accetta l’ipotesi nulla H₀ della non differenza tra gruppi a confronto, quando invece essi sono differenti.

Proprio da queste due possibili tipologie di errore, legate alle inferenze suggerite dai risultati di uno studio, derivano altri due elementi indispensabili per stabilire la numerosità campionaria: il livello di confidenza e la potenza dello studio.

Il livello di confidenza definisce l’intervallo di valori entro il quale si può essere “ragionevolmente” sicuri che l’effetto rilevato non sia dovuto al caso; di solito è fissato al 95%, valore che corrisponde a un p-value (p) di 0.05. Il p-value esprime la probabilità di commettere un errore di tipo I (α), misurando la probabilità che la differenza osservata tra gruppi a confronto possa essere dovuta al caso, se l’ipotesi nulla è vera. Se si sceglie un livello di confidenza più elevato del 95% nel rilevare un effetto desiderato, è necessaria una maggiore dimensione del campione, in quanto il livello di confidenza dipende dall’errore standard che a sua volta cresce col reciproco della numerosità campionaria.

La potenza dello studio, o potenza statistica, rappresenta il complemento a 1 dell’errore di tipo II (1-β) e misura la probabilità di rifiutare l’ipotesi nulla H₀ (non differenza tra gruppi a confronto) quando essa è falsa e di accettare, quindi, l’ipotesi alternativa H₁ (differenza tra gruppi a confronto) quando essa è vera. Di solito si ritiene accettabile un errore di II tipo non superiore a 0.20 corrispondente a una potenza dello studio pari a 0.80. Il campione necessario aumenta se aumenta la potenza richiesta (1-β aumentato). Si tenga presente che esiste una relazione ben precisa tra α, β e numerosità campionaria, in quanto quando due dei tre valori sono noti, l’altro è determinato. Per un dato livello di significatività α, all’aumentare della dimensione del campione, si ridurrà β (aumenta la potenza dello studio). Per una data dimensione campionaria, al crescere del livello di significatività α diminuirà β (aumenta la potenza dello studio), mentre al decrescere di α aumenterà β (diminuisce la potenza dello studio).

Nel calcolo della corretta dimensione campionaria il ricercatore deve allora specificare i valori relativi alla varianza attesa, all’alfa desiderato (errore di tipo I), alla più piccola differenza clinicamente rilevante e, di solito, al beta desiderato (errore di tipo II) (3).

Il calcolo della dimensione campionaria, quindi, svolge un ruolo di fondamentale importanza nel garantire il successo degli studi clinici.

Una corretta dimensione campionaria non solo assicura la validità delle sperimentazioni cliniche, ma assicura anche che le sperimentazioni pianificate avranno la potenza desiderata per rilevare correttamente una differenza clinica significativa se tale differenza esiste davvero (4).

Il calcolo della dimensione campionaria dipende dal tipo di studio epidemiologico che si vuole intraprendere: descrittivo, osservazionale o controllato randomizzato. A ogni tipo di studio corrisponde una specifica formula di calcolo della dimensione campionaria, per il reperimento e la descrizione della quale si rimanda alla letteratura specializzata e ad alcuni articoli esemplificativi in materia di campionamento (5).

Di seguito si riportano tre esempi di calcolo della dimensione campionaria nei casi di: schema di campionamento casuale semplice senza ripetizione, schema di campionamento casuale semplice con ripetizione e schema di campionamento casuale semplice da una popolazione con numerosità molto elevata.

Esempio 1

Nel 2010 uno studio effettuato su una popolazione di 5.000 persone (uomini e donne) nella fascia di età 30-70 anni ha rilevato una prevalenza di coronaropatia pari al 6%. Volendo effettuare nel 2020 nella stessa popolazione una stima campionaria della prevalenza di coronaropatia accettando un errore (E) del 2% quanti soggetti dovranno essere esaminati se la stima derivante dal campione deve cadere entro 2 punti percentuali rispetto alla vera prevalenza, con un livello di confidenza (1-α) pari al 95%?

Disegno (schema) di campionamento: campionamento casuale semplice senza ripetizione

N	=	5.000 (numero di persone nella popolazione, uomini e donne, nella fascia di età 30-70 anni)
z	=	1,96 (quantile della normale standardizzata corrispondente al livello di confidenza (1 – α) = 95%)
p	=	6% (prevalenza derivata da uno studio precedente)
q	=	(1-p) = 0,94
E	=	2% (errore ammesso per la stima derivante dal campione)

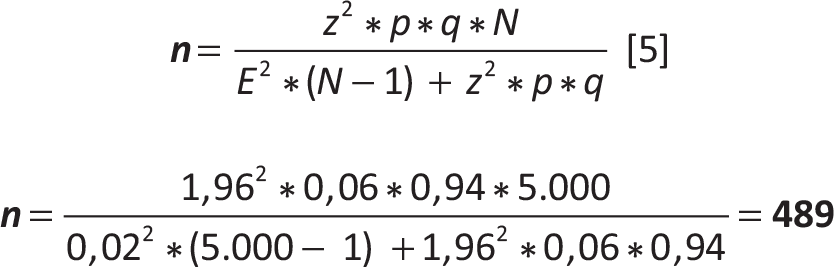
Con un campione di 489 persone appartenenti alla fascia di età 30-70 anni, tratte con uno schema di campionamento casuale semplice senza ripetizione da una popolazione di 5.000 persone della stessa fascia di età, vi sarà una probabilità del 95% che i risultati del campione siano validi con un margine d’errore del 2%.

Esempio 2

Disegno (schema) di campionamento: campionamento casuale semplice con ripetizione

z	=	1,96 (quantile della normale stand. corrispondente al livello di confidenza (1 – α) = 95%)
p	=	6% (prevalenza derivata da uno studio precedente)
q	=	(1-p) = 0,94
E	=	2% (errore ammesso per la stima derivante dal campione)

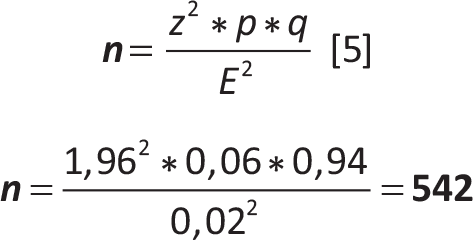
Con un campione di 542 persone appartenenti alla fascia di età 30-70 anni, tratte con uno schema di campionamento casuale semplice con ripetizione da una popolazione di 5.000 persone della stessa fascia di età, vi sarà una probabilità del 95% che i risultati del campione siano validi con un margine d’errore del 2%.

Esempio 3

Si vuole pianificare un esperimento su un nuovo farmaco per la cura di una patologia X. Dati preliminari sull’utilizzo del nuovo farmaco suggeriscono una attenuazione o scomparsa dei sintomi patologici nel 90% dei casi mentre con l’utilizzo del farmaco standard (utilizzato come controllo) tale percentuale risulta essere pari all’80%. Quanti pazienti bisogna includere nel gruppo dei trattati con il nuovo farmaco e in quello dei trattati con il farmaco standard per rilevare questo miglioramento del 10% dovuto all’utilizzo del nuovo farmaco con un livello di significatività pari al 5% (e quindi un livello di confidenza del 95%) ed una potenza del 90%?

Disegno (schema) di campionamento: campionamento casuale semplice da una popolazione con numerosità molto elevata

zα	=	1,96 (quantile della normale stand. per l’errore alfa)
zβ	=	1,282 (quantile della normale stand. per l’errore beta)
p0	=	80% (% di attenuazione o scomparsa dei sintomi patologici con il farmaco standard)
p1	=	90% (% di attenuazione o scomparsa dei sintomi patologici con il nuovo farmaco)
π	=	(p0 + p1)/2 = 0,85
E	=	2% (errore ammesso per la stima derivante dal campione)

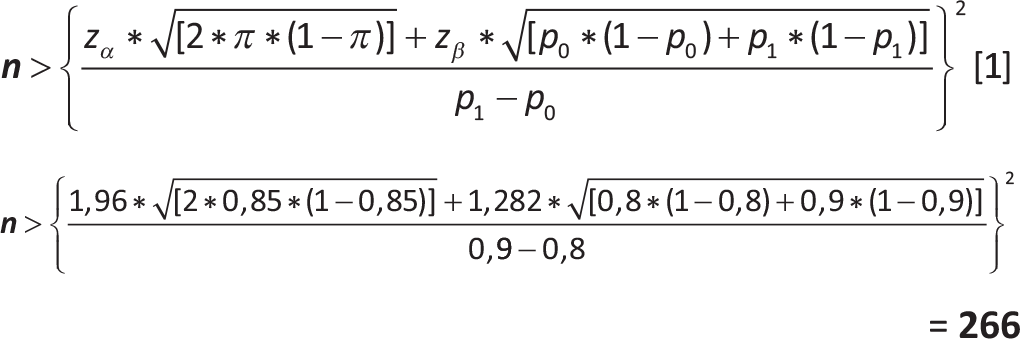
Per rilevare un miglioramento del 10% dei casi con una attenuazione o scomparsa dei sintomi patologici dovuto all’utilizzo del nuovo farmaco con un livello di significatività pari al 5% (e quindi un livello di confidenza del 95%) ed una potenza del 90% occorre reclutare almeno 266 pazienti per gruppo.